Depth-first Search
Overview
DFS traverses or searches tree or graph data structures. It starts at the root node (selecting some arbitrary node in the case of a graph) and explores as far as possible along each branch before backtracking.
It allows to find the shortest path from a start to a target node in unweighted graphs.
Extra memory, usually a stack, is needed to keep track of the nodes discovered so far along a specified branch which helps in backtracking.
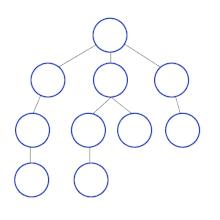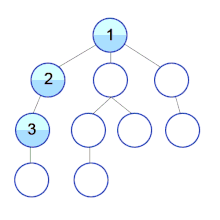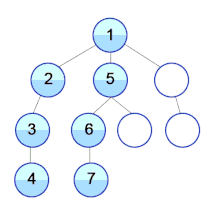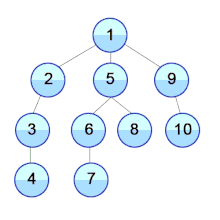
Pseudocode
Recursive
DFS(G, v) is
label v as discovered
for all directed edges from v to w that are in G.adjacentEdges(v) do
if vertex w is not label as discovered then
DFS(G, w)
Iterative
DFS_iterative(G, v) is
let S be a stack
S.push(v)
while S is not empty do
v = S.pop()
if v is not labeled as discovered then
label v as discovered
for all edges from v to w in G.adjacentEdges(v) do
s.push(w)
Time & space complexity
| When traversing an entire graph, it takes time $O( | V | + | E | )$, where $ | V | $ is the number of vertices and $ | E | $ the number of edges. It also uses space $O( | V | )$ in the worst case to store the stack of vertices on the current search pat as well as the set of already-visited vertices. |
Thus, time and space bounds are the same as for BFS and the choice of which of these to use depends on the different properties of the vertex ordering the two produce.
Non-termination
In specific domains, such as searching for solutions in AI or web-crawling, the graph to be traversed is often either too large to visit in its entirety or infinite. In such cases, search is only performed to a limited depth. Also, due to limited resources, one typically does not use data structures to keep track of the set of all previously visited vertices.
When an appropriate depth limit is not known a priori, iterative deepening depth-first search applies DFS repeatedly with a sequence of increasing limits.
Vertex ordering - Graph traversal
DFS can be used to linearly order the vertices of a graph or tree.
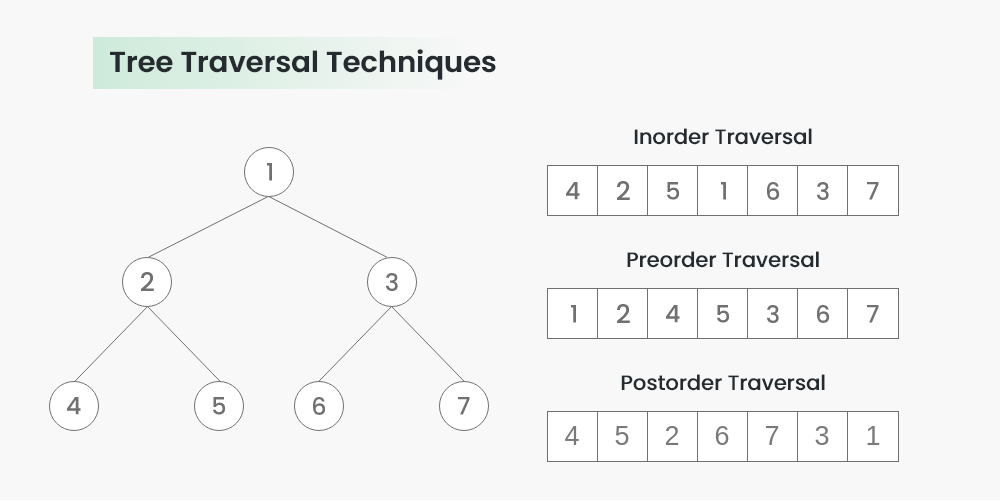
- preordering: in the order that they were first visited by DFS.
- postordering: in the order that they were last visited by DFS.
- inorder: traverse the left subtree, then the root, and then the right subtree.
- reverse preordering: in the opposite order of their first visit.
- reverse postordering: in the opposite order of their last visit.