Graph

• Graph
  • Overview
  • Directed and Undirected Graphs
  • Representation
    • Adjacency-list representation

Overview

In mathematics, and more specifically in graph theory, a graph is a structure amounting to a set of objects in which some pair of the objects are in some sense “related”.

The object correspond to mathematical abstractions called vertices (also nodes or points), and each of the related pairs of vertices is called an edge (also link or line)

Directed and Undirected Graphs

The edges may be directed or undirected. For example, if the vertices represent people at a party, and there is an edge between two people if they shake hands, then this graph is undirected because any person A can shake hands with a person B only if B also shakes hands with A.

In contrast, if any edge from a person A to a person B corresponds to A owes money to B, then this graph is directed, because owing money is not necessarily reciprocated.

The former type of graph is called an undirected graph while the latter type of graph is called a directed graph.

Representation

There are two standard ways to represent a graph $G = (V, E)$, either directed or undirected:

1. Collection of adjacency lists.
2. Adjacency matrix.

Because adjacency-list representation provides a compact way to represent sparse graphs - those for which $

E

$ is much less than $

V

^2$ - it is usually the method of choice.

We may prefer an adjacency-matrix representation when the graph is dense ($

E

$ is close to $

V

^2$) or when we need to be able to tell quickly if there is an edge connecting two given vertices.

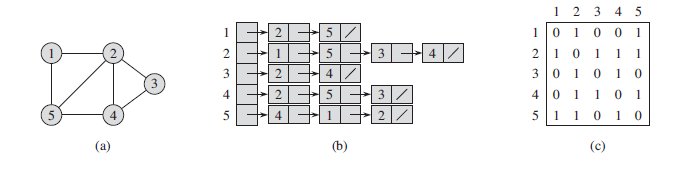
(a) An undirected graph G with 5 vertices and 7 edges. (b) An adjacency-list representation of G. (c) The adjacency-matrix representation of G.

(a) A directed graph G with 6 vertices and 8 edges. (b) An adjacency-list representation of G. (c) The adjacency-matrix representation of G.

Adjacency-list representation

The adjacency-list representation of a graph G = (V, E) consists of an array Adj of _

V

_ lists, one for each vertex in V. For each $u \in V$, the adjacency list Adj[u] contains all the vertices v such that there is an edge $(u,v) \in E$. That is, Adj[u] consists of all the vertices adjacent to u in G.