Van Emde Boas Trees

Overview

A Van Emde Boas (vEB) tree is a data structure that supports operations on a dynamic set of $n$ integers from a bounded universe of size $u$. The universe size $u$ is typically expressed as $2^w$ for some integer $w$, which means $u = 2^w$.

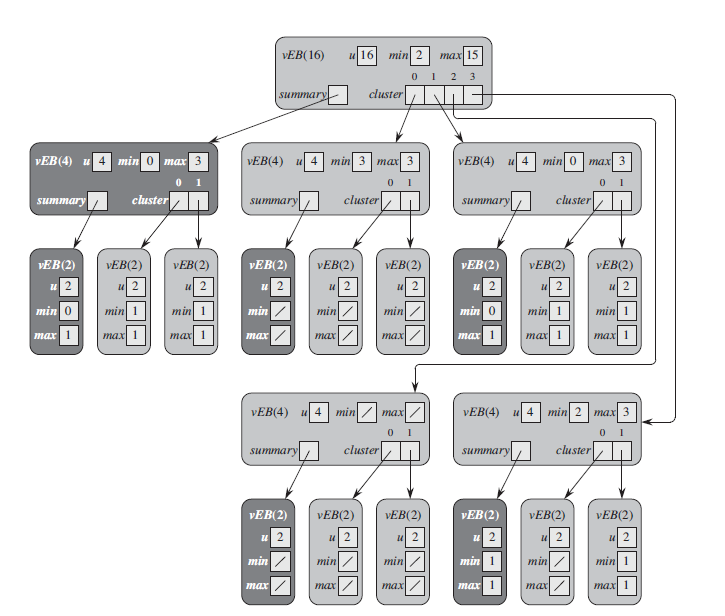
Structure

A vEB tree for a universe of size $u$ can be thought of as a recursive structure:

• If $u = 2$, the vEB tree is a simple base case where it can hold only two elements, and operations can be performed in constant time.

• If $u > 2$, the vEB tree is divided into two levels: a top level and a bottom level.

  • The top level, or summary, is a vEB tree of size $\sqrt{u}$.
  • The bottom level consists of $\sqrt{u}$ clusters, each of size $\sqrt{u}$.

Operations

The key operations supported by a Van Emde Boas tree include the Priority Queue operations:

• Insertion
• Deletion
• Membership query (contains)
• Successor query (finding smallest element larger than a given element)
• Minimum
• Maximum

Insertion

1. Determine the cluster in which $x$ belongs, i.e., $x$ is mapped to a cluster index $\lceil{x / \sqrt{u}} \rceil$ and a position within the cluster $pos = x \mod \sqrt{u}$.
2. Recursively insert $pos$ into the corresponding cluster.
3. If the cluster was previously empty, update the summary to reflect the presence of this cluster.

Deletion

1. Determine the cluster and position within the cluster as in insertion.
2. Recursively delete $pos$ from the corresponding cluster.
3. If the cluster becomes empty, update the summary to reflect the absence of this cluster.

Membership query

To check if an element $x$ is present:

1. Determine the cluster and position.
2. Recursively check for membership in the corresponding cluster.

Successor/Predecessor

1. Determine the cluster and position.
2. Recursively find the successor or predecessor within the cluster or use the summary to jump to the next non-empty cluster if necessary.

Time complexity

The time complexity for each operation in a vEB tree is determined by the depth of the recursion. Each recursive step reduces the universe size from $u$ to $\sqrt{u}$. The number of recursive steps needed to reduce $u$ down to 2 is $log log u$. This is because: $log log u = log log(2^w) = log w = O(log log u)$.

Therefore, the time complexity of those operations is $O(log log u)$, where $u$ is the size of the universe.

This is significantly better than the $O(log n)$ time complexity provided by balanced binary search trees (BSTs) when $u$ is much larger than $n$.