Depth-first Search

• Depth-first Search
  • Overview
  • Time complexity
  • Use cases
  • Base Algorithm
    • Apply to Arbitrary Trees
  • Orders (types)
    • Pre-order: NLR (red)
    • Post-order: LRN (blue)
    • In-order: LNR (green)
    • Reverse pre-order: NRL
    • Reverse post-order: RLN
    • Reverse in-order, RNL

Overview

In DFS the search tree is deepened as much as possible before going to the next sibling.

Depth-first search is easily implemented via a stack, including recursively (via the call stack).

Time complexity

Depth-first search visits every vertex once and checks every edge in the graph once. Therefore, DFS complexity is $O(

V

+

E

)$.

It is mos space-efficient than breadth-first search because BFS keeps a priority queue of the entire frontier while DFS maintains a few pointers at each level.

Use cases

Depth-first search is used in:

• Topological sorting.
• Scheduling problems.
• Cycle detection in graphs (e.g., spanning trees, mapping routes).
• Solving puzzles with only one solution (e.g., maze, sudoku).

Base Algorithm

Perform the following operations at each node:

1. If the current node is empty then return.
2. Execute the following three operations in a certain order:
   1. (N) Visit the current node.
   2. (L) Recursively traverse the current node’s left subtree.
   3. (R) Recursively traverse the current node’s right subtree.

Apply to Arbitrary Trees

To traverse arbitrary trees (not necessarily binary trees) with depth-first search, perform the following operations at each node:

1. If the current node is empty then return.
2. Visit the current node for pre-order traversal.
3. For each i from 1 to the current node’s number of subtrees - 1, or from the latter to the former for reversal traversal, do:
   1. Recursively traverse the current node’s i-th subtree.
   2. Visit the current node for in-order traversal.
4. Recursively traverse the current node’s last subtree.
5. Visit the current node for post-order traversal.

Orders (types)

There are three common ways to traverse them in depth-first order: in-order, pre-order and post-order. Beyond these basic traversals, various more complex or hybrid schemes are possible, such as depth-limited searches like iterative deepening depth-first search.

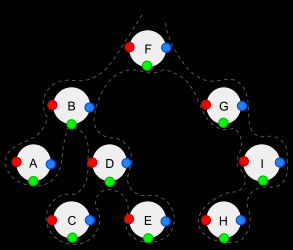
Depth-first traversal (dotted path) of a binary tree:

• Pre-order (node visited at position red): F, B, A, D, C, E, G, I, H
• In-order (node visited at position green): A, B, C, D, E, F, G, H, I
• Post-order (node visited at position blue): A, C, E, D, B, H, I, G, F

Pre-order: NLR (red)

1. Visit current node
2. Recursively traverse left subtree
3. Recursively traverse right subtree

The pre-order traversal is a topologically sorted one, because a parent node is processed before any of its child nodes is done.

Post-order: LRN (blue)

1. Recursively traverse left subtree
2. Recursively traverse right subtree
3. Visit the current node

In-order: LNR (green)

1. Recursively traverse left subtree
2. Visit the current node
3. Recursively traverse right subtree

Reverse pre-order: NRL

1. Visit current node
2. Recursively traverse right subtree
3. Recursively traverse left subtree

Reverse post-order: RLN

1. Recursively traverse right subtree
2. Recursively traverse left subtree
3. Visit the current node

Reverse in-order, RNL

1. Recursively traverse right subtree
2. Visit the current node
3. Recursively traverse left subtree

In a binary search tree ordered such that in each node the key is greater than all keys in its left subtree and less than all keys in its right subtree, reverse in-order traversal retrieves the keys in descending sorted order.