M-ary tree

• Overview
• Unbounded Branching
• Types
• Design & Implementation
  • Arrays
  • Pointer-based
  • Unbounded branching

Overview

In graph theory, an M-ary tree (also known as K-ary or K-way tree) is a rooted tree in which each node has no more than $m$ children.

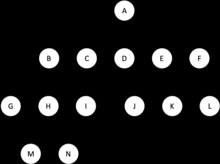
An example of a m-ary tree with m=5.

Types

• Full: Each node has either 0 or $m$ children.

• Complete: Every level, except possible the last is completely filled, and all nodes in the last level are as far left as possible. It is maximally space efficient.

• Perfect: Full m-ary tree in which all leaf nodes are at the same depth.

Common usages

• File systems.
• Database indexing (particularly B-trees, a type of M-ary tree).
• Routing tables.
• Prefix trees (also known as Tries).
• Symbol tables.
• Compression algorithms.

Design & Implementation

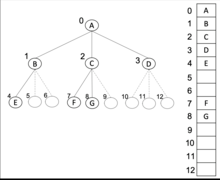
Arrays

Stored in breadth-first order as an implicit data structure in arrays, and if the tree is a complete tree, this method wastes no space.

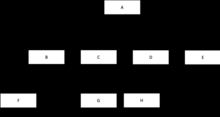
Pointer-based

Each node would have an internal array for storing pointers to each of its $m$ children.

Unbounded branching

We can represent any class of trees in which the number of children of each node is at most some constant k. We replace left and right attributes by child_1, ..., child_k.

This scheme no longer works when the number of children of a node is unbounded, since we do not know how many attributes to allocate in advance. Moreover, even if the number of children $k$ is bounded by a large constant, but most nodes have a small number of children, we may waste a lot of memory.

Fortunately, there is a clever scheme to represent trees with arbitrary numbers of children, using only $O(n)$ space for any n-node rooted tree.

Each node contains a parent pointer p, and T.root points to the root of tree $T$. Instead of having a pointer to each children, however, each node $x$ has only two pointers:

1. x.left-child points to the leftmost child of node x
2. x.right-sibiling points to the sibling of x immediately to its right.