Fibonacci Heaps

• Fibonacci Heaps
  • Definition
  • Operations
  • Structure
  • Theoretical standpoint
  • Practical standpoint

Definition

The Fibonacci heap data structure serves a dual purpose:

1. It supports a set of operations that constitutes what is known as a mergeable heap.
2. Several of its operations run in constant amortized time, which makes this data structure well suited for applications that invoke these operations frequently.

Operations

In addition to the mergeable heap five operations, Fibonacci Heaps also support the following two operations:

• $DECREASE-KEY(H, x, k)$: Assigns to element x within heap H the new key value k, which we assume to be no greater than its current key value.

• $DELETE(H, x)$: Deletes element x from heap H.

We are considering mergeable min heaps. Alternatively, we could define a mergeable max heap with the operations MAXIMUM, EXTRACT-MAX, and INCREASE-KEY.

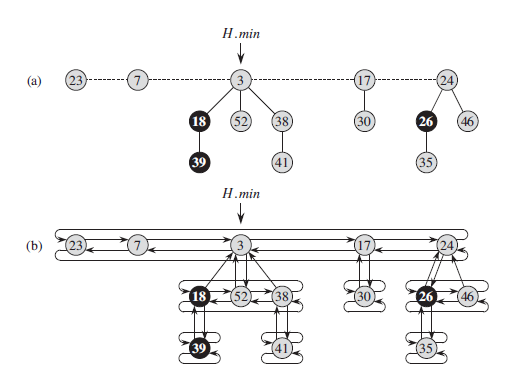
Structure

A Fibonacci heap is a collection of rooted trees that are min-heap ordered. That is, each tree obeys the min-heap property

Theoretical standpoint

Fibonacci heaps are specially desirable when the number of EXTRACT-MIN and DELETE operations is small relative to the number of operations performed.

Fast algorithms for problems such as computing minimum spanning trees and finding single-source shortest paths make essential use of Fibonacci heaps.

Practical standpoint

Constant factors and programming complexity of Fibonacci heaps make them less desirable than ordinary binary/k-ary heaps for most applications, except for certain applications that manage large amounts of data. Thus, they are predominantly of theoretical interest.