Binary Heap
Overview
The Binary Heap is a Binary Tree with the following properties:
- It is a Complete Tree. This property makes Heap suitable to be stored in an array.
In a Complete Tree, all levels are completely filled except possibly for the last level, and the last level has all keys as left as possible.
- It is either Min Heap or Max Heap, the same property must be recursively true for all nodes in the tree.
In a Min Binary Heap, the key at root must be minimum among all keys present in the Binary Heap. Max Binary Heap is the opposite.
10 10
/ \ / \
20 100 15 30
/ / \ / \
30 40 50 100 40
Applications
-
Heap Sort uses Binary Heap to sort an array in
O(n log n) time. -
Priority Queues can be efficiently implemented using Binary Heap because it supports
insert,delete,extractMax,decreaseKeyoperations inO(log n)time. -
Graph Algorithms use priority queues in algorithms like Dijkstra’s Shortest Path and Prim’s Minimum Spanning Tree.
-
Many problems can be efficiently solved using Heaps.
- K’th Largest Element in an Array
- Sort an almost sorted array
- Merge K Sorted Arrays
Height
Viewing a heap as a tree, we define the height of a node in a heap to be the number of edges on the longest simple downward path from the node to a leaf, and we define the height of the heap to be the height of its root.
Since a heap of n elements is based on a complete binary tree, its height is Theta(n).
Types & Heap Property
There are two kinds of binary heaps, max-heaps & min-heaps. In both kinds, the values in the nodes satisfy a heap proprety.
Max Heap
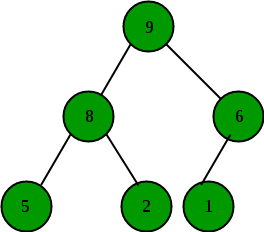
In a max-heap property is that for every node i other than the root:
A[PARENT(i)] >= A[i]
That is, the value of a node is at most the value of its parent. Thus, the largest element in a max-heap is stored at the root4, and the subtree rooted at a node contains values no larger than that contained as the node itself.
Min Heap
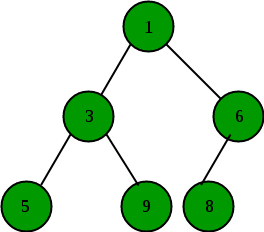
A min-heap is organized in the opposite way, the min-heap property is that for every node i other than the root:
A[PARENT(i)] <= A[i]
The smallest element in a min-heap is at the root.
Operations
-
MAX-HEAPIFY procedure, which runs in O(lg n) time, is the key to maintaining the max-heap property.
-
BUILD-MAX-HEAP procedure, which runs in O(n) time, procedues a max-heap from an unordered input array.
-
MAX-HEAP-INSERT, HEAP-EXTRACT-MAX, HEAP-INCREASE-KEY, HEAP-MAXIMUM procedures, which run in O(lg n) time, allow the heap data structore to imlement a priority queue.
Get Relative Index
PARENT(i): return Floor(i/2)
LEFT(i): return 2i
RIGHT(i): return 2i + 1
Time complexity
- Insertion: $O(log n)$
- Deletion (remove-min or remove-max): $O(log n)$
- Peek (find-min or find-max): $O(1)$
- Extract-min or extract-max: $O(log n)$
- Decrease-key or increase-key: $O(log n)$
- Build heap: $O(n)$
Traversal
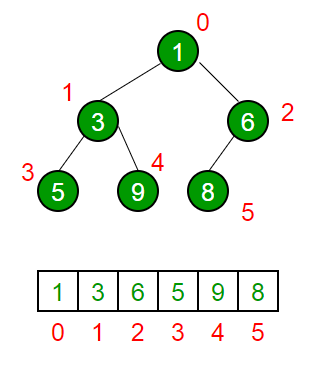
Maintaining the heap property
When MAX-HEAPIFY is called, it assumes that the binary trees rooted at LEFT(i) and RIGHT(i) are max heaps, but that A[i] might be smaller than its children, thus violating the max-heap property. MAX-HEAPIFY lets the value at A[i] “float-down” in the max-heap so that the subtree rooted at index i obeys the max-heap property.
MAX-HEAPIFY(A, i):
l = LEFT(i)
r = RIGHT(i)
if l <= A.heap-size and A[l] > A[i]
largest = l
else largest = i
if r <= A.heap-size and A[r] > A[largest]
largest = r
if largest != i
exchange A[i] with A[largest]
MAX-HEAPIFY(A, largest)
This takes O(lg n) time.
Building a heap
We can use the MAX-HEAPIFY procedure in a bottom-up manner to convert an array A[1..n], into a max-heap.
The elements in the subarray A[(n/2 + 1)..n] are all leaves of the tree, and so each is a 1-element heap to begin with. The procedure BUILD-MAX-HEAP goes through the remaining nodes of the tree and runs MAX-HEAPIFY on each one.
BUILD-MAX-HEAP(A):
A.heap-size = A.length
for i = [A.length/2] downto 1
MAX-HEAPIFY(A, i)
Each call to MAX-HEAPIFY costs O(lg n) time, and BUILD-MAX-HEAP makes O(n) such calls, thus the running time is O(n lg n). This upper bound, though correct, is not asymptotically tight.
We can prove the running time of BUILD-MAX-HEAP is O(n).
Other Procedures
HEAP-MAXIMUM(A)
return A[1]
HEAP-EXTRACT-MAX(A) // O(lg n)
if A.heap-size < 1
error "heap underflow"
max = A[1]
A[1] = A[A.heap-size]
A.heap-size = A.heap-size - 1
MAX-HEAPIFY(A, 1)
return max
HEAP-INCREASE-KEY(A, i, key) // O(lg n)
if key < A[i]
error "new key is smaller than current key"
A[i] = key
while i > 1 and A[PARENT(i)] < A[i]
exchange A[i] with A[PARENT(i)]
i = PARENT(i)
MAX-HEAP-INSERT(A, key) // (lg n)
A.heap-size = A.heap-size + 1
A[A.heap-size] = -infinity
HEAP-INCREASE-KEY(A, A.heap-size, key)