Binary Search Tree

Binary Search Tree
- Overview
- BST Property
- Algorithms
  - Inorder tree walk
  - Preorder tree walk
  - Postorder tree walk
  - Searching
  - Max & Min
  - [Successor & Predecessor O(h)](#successor–predecessor–oh)
    - Important Child Property
  - [Insertion O(h)](#insertion–oh)
  - Deletion
- Randomly built BST

Overview

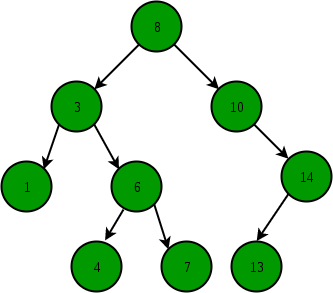
A BST is organized in a binary tree. We can represent such a tree by a linked data structure in which each node is an object. In addition to a key and satellite data, each node contains attributes left, right and p that point to the nodes corresponding. If a child or the parent is missing, the appropriate attribute contains the value NIL.

Basic operations on a BST take time proportional to the height of the tree. For a complete BST with n nodes, such operations run in $O(lg n)$ worst-case time. If the tree is a linear chain of n nodes, however, the same operations take $O(n) worst-case time. Luckily, the expected height of a randomly built BST is $O(lg n)$, so basic dynamic-set operations on such a tree take $O(lg n)$ time on average.

BST Property

The keys in a BST are always stored in such a way as to satisfy the binary-search-tree property.

Let x be a node ina BST. If y is a node in the left subtree of x, then y.key <= x.key. If y is a node in the right subtree of x, then y.key >= x.key.

Algorithms

Inorder tree walk

The BST property allows us to print out all the keys in a BST in sorted order by a simple recursive algorithm, called an inorder tree walk. This prints the key of the root of a subtree between printing the values in its left subtree and printing those in its right subtree.

INORDER-TREE-WALK(x):
    if x != NIL
        INORDER-TREE-WALK(x.left)
        print x.key
        INORDER-TREE-WALK(x.right)

Preorder tree walk

Prints the root before the values in either subtree

Postorder tree walk

Prints the root after the values in its subtrees.

Searching

Given a pointer to the root of the tree and a key k, the following returns a pointer to a node with key k if one exists, otherwise, it returns NIL.

TREE-SEARCH(x, k)
    if x == NIL or k == x.key:
        return x
    if k < x.key
        return THREE-SEARCH(x.left, k)
    else return TREE-SEARCH(x.right, k)

ITERATIVE-TREE-SEARCH(x, k)
    while x != NIL and k != x.key:
        if k < x.key
            x = x.left
        else x = x.right
    return x

Max & Min

TREE-MINIMUM(x)
    while x.left != NIL
        x = x.left
    return x

TREE-MAXIMUM(x)
    while x.right != NIL
        x = x.right
    return x

Successor & Predecessor ($O(h)$)

Given a node in a BST, sometimes we need to find its successor in the sorted order determined by an inorder tree walk.

If all keys are distinct, the successor of a node x is the node with the smallest key greater than x.key. The following returns the successor of a node x in a BST if it exists, and NIL if x hast he largest key in the tree.

TREE-SUCCESSOR(x)
    if x.right != NIL
        return TREE-MINIMUM(x.right)
    y = x.p
    while y != NIL and x == y.right
        x = y
        y = y.p
    return y

We break the code into two cases. If the right subtree of node x is nonempty, then the successor of x is just the leftmost node in x’s right subtree. On the other hand, if the right subtree of node x is empty and x has a successor y, then y is the lowest ancestor of x whose left child is also an ancestor of x.

Important Child Property

If a node in a BST has two children, then its successor has no left child and its predecessor has no right child.

Insertion ($O(h)$)

This procedure takes a node z for which z.key = v and z.left = z.right = NIL. It inserts z into an appropriate position in the tree.

TREE-INSERT(T, z)
    y = NIL
    x = T.root
    while x != NIL
        y = x
        if z.key < x.key
            x = x.left
        else x = x.right
    z.p = y
    if y == NIL         // tree T was empty
        T.root = z
    else if z.key < y.key
        y.left = z
    else y.right = z 

Deletion

The strategy for deleting a node z from a BST T has four basic cases:

CASE 1: If z has no children, then we simply remove it by modifying its parent to replace z with NIL.
CASE 2: If z has just one child, then we elevate that child to take z’s position in the tree by modifying z’s parent.
CASE 3/4: If z has two children, the we find z’s successor y, which must be in z’s right subtree, and have y take z’s position in the tree. The rest of z’s original right subtree becomes y’s new right subtree, and z’s left subtree becomes y’s new left subtree. This case is the tricky one, because, it matters whether y is z’s right child.

The procedure for deleting a given node z from a BST T takes as arguments pointers to T and z. It organizes its cases a bit differently from the three cases outlined previously by considering the four cases.

If z has no left child, then we replace z by its right child (CASE 2), which may or may not be NIL (CASE 1).
If z has just one child, which is its left child (CASE 2), then we replace z by its left child.
Otherwise, z has both a left and a right child (CASE 3/4). We find z’s successor y, which lies in z’s right subtree and has no left child (see Successor & Predecessor). We want to splice y out of its current location and have it replace z in the tree.
1. If y is z’s right child, then we replace z by y, leaving y’s right child alone.
2. Otherwise, y lies within z’s right subtree but is not z’s right child. In this case, we first replace y by its own right child, and then we replace z by y.

We define a subroutine TRANSPLANT, which replaces one subtree as a child of its parent with another subtree.

TRANSPLANT(T, u, v)
    if u.p == NIL       // tree was empty or only 'u' had root
        T.root = v
    else if u == u.p.left       // put subtree in 'u' parent's left child
        u.p.left = v
    else u.p.right = v          // put subtree in `u` parent's right child
    if v != NIL                 // finally, replace `v`'s parent
        v.p = u.p

Now, to delete a node z from BST T:

TREE-DELETE(T, z)
    if z.left == NIL
        TRANSPLANT(T. z, z.right)       // CASE 1 or 2
    else if z.right == NIL
        TRANSPLANT(T, z, z.left)        // CASE 2
    else y = TREE-MINIMUM(z.right)      // we find z's successor
        if y.p != z                     // CASE 4, z's sucessor (y) is not z's right child
            TRANSPLANT(T, y, y.right)   // we replace y, with y's right child
            y.right = z.right           // we replace z with y (we start by replacing y's right subtree with z's right subtree)
            y.right.p = y
        TRANSPLANT(T, z, y)             // then we replace z with y, meaning we still have z's right child, and now we are also bringing y's left subtree if any
        y.left = z.left
        y.left.p = y

Randomly built BST

So far, little is known about the average height of a BST when both insertion and deletion are used to create it.

We can define a randomly built BST on

keys as one that arises from inserting the keys in random order into an initially empty tree, where each of the n! permutations of the input keys is equally likely.

The expected height of a randomly built BST on n distinct keys is O(lg n).

algorithms

Algorithms Handbook