Array
Overview
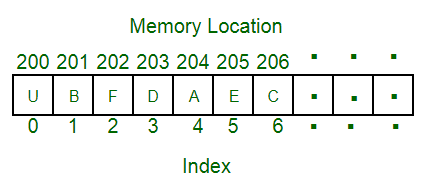
An array is a collection of items stored at contiguous memory locations. The idea is to store multiple items of the same type together. This makes it easier to calculate the position of each element by simply adding an offset to a base value (i.e., the memory location of the first element of the array).
Applications
- Store data elements of the same data type.
- CPU Scheduling.
- Implement other data structures like Stacks, Queues, Heaps, Hash tables, etc.
Algorithms & Techniques
Two-Pointer traversal
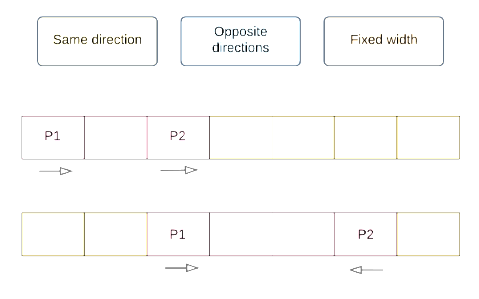
Two pointers help us cover a sub-array within the main array.
The strength of this technique is that we will never have more than $𝑂(𝑛)$ iterations for the while loop because the pointers start $𝑛$ away from each other and move at least one step closer in every iteration. Therefore, if we can keep the work inside each iteration at $𝑂(1)$, we’ll have linear runtime.
Sliding window
The algorithm
In sliding window, we maintain two variables left and right, which at any given time
represent the current subarray under consideration. For expanding the size of the window,
we increase right. For shrinking the window, we increase left.
function fn(arr):
left = 0
for (int right = 0; right < arr.length; right++):
Do some logic to "add" element at arr[right] to window
while WINDOW_IS_INVALID:
Do some logic to "remove" element at arr[left] from window
left++
Do some logic to update the answer
When the window must have a fixed size k:
function fn(arr, k):
curr = some data to track the window
// build the first window
for (int i = 0; i < k; i++)
Do something with curr or other variables to build first window
ans = answer variable, probably equal to curr here depending on the problem
for (int i = k; i < arr.length; i++)
Add arr[i] to window
Remove arr[i - k] from window
Update ans
return ans
Problems
There is a very common group of problems involving subarrays that can be solved efficiently with sliding window.
First, the problem will either explicitly or implicitly define criteria that make a subarray “valid”. There are 2 components regarding what makes a subarray valid:
- A constraint metric: Some attribute of the array such as the number of unique elements, their frequency, etc.
- A numeric restriction on the constraint metric.
Second, the problem will ask you to find subarrays in some way:
- The most common task is to find the best valid subarray based on some criteria.
- Find the number of valid subarrays.
Some examples of common problems are:
- Find the longest subarray with at most K distinct elements.
- Find the longest subarray with the sum less than or equal to
k. - Find the longest substring that has at most one
0. - Find the number of subarrays that have a product less that
k.